鉱物学の勉強をしているので、立体図形の対称性について自分なりの理解をまとめてみました。
小学校の算数でやる平面図形の線対称、点対称の概念を拡張すれば、イメージがつかみやすいんじゃないかと。
正八面体を題材に考えていきたいと思います。
説明のために正八面体の頂点を次のようにA~Fとふります。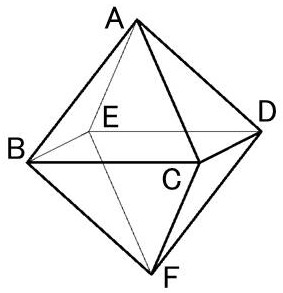
対称面
対称面とは、平面図形だと線対称の対象軸にあたるものです。
つまり対称面や対象軸をが鏡となって左右が同じ形になるものです。「鏡映対称性」なんて言われることもあります。
すると、正八面体の対称面は、
6つの頂点のうち、AとFのような(*1)対向する頂点をのぞいた4つの頂点でできる正方形の面が3つと、
(*1)AとFのほか、BとD、CとEと3組あるので、正方形の対称面も3つあります。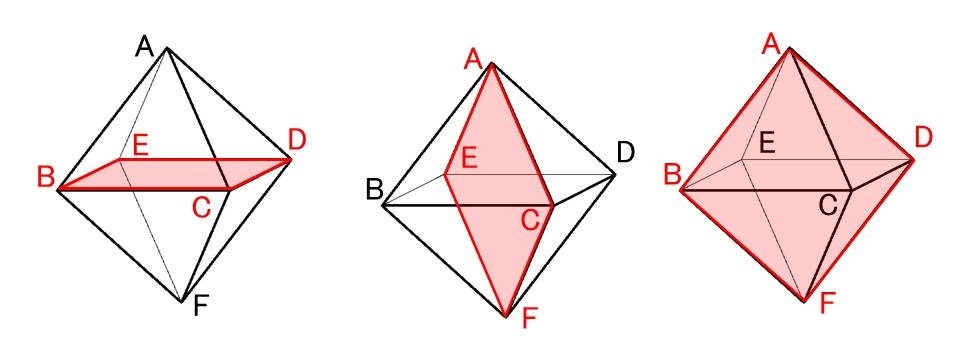
対向する頂点2つと、残りの4つの頂点でできる正方形のうち平行な2辺それぞれの中点を結んでできるひし形も対称面になります。これは対向する頂点の選び方が3通り。そして正方形の平行な2辺の選び方が(たとえば正方形BCDEを考えるとBCとED、BEとCDの)2通りあるので、3×2=6通りあります。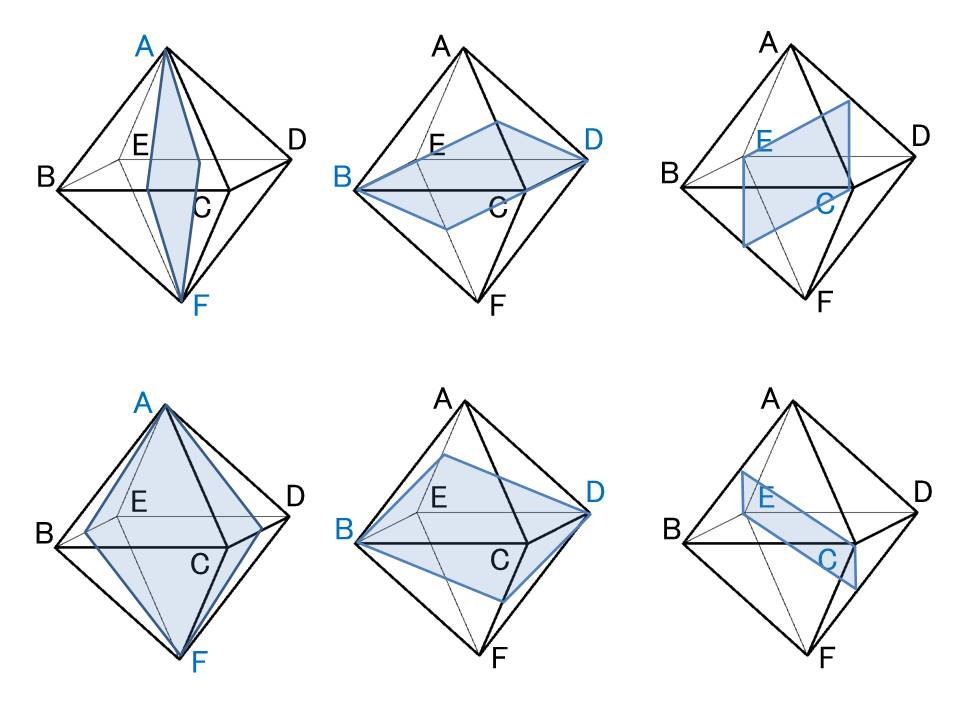
あわせて9つの対称面をもちます。
対称軸
平面図形で「対称軸」といえば、線対称で登場しますが、立体図形の対称軸は、平面図形でいえば、線対称よりもむしろ点対称の方がイメージ的に近いです。
平面図形で点対称といえば、SとかNの文字みたいに1つの点を中心にして180°回すと、もとの図形にぴったり重なる図形を言います。このときの「1つの点」が対象の中心です。
ところでこの図形、線対称でも点対称でもありません。
だけど赤い点を中心に120°、つまり1/3回転するともとの図形にぴったり重なります。
もっというと、1回転する間に、120°、240°、360°回転したときの3回、もとの図形にぴったり重なります。
同じことを正方形でやると1回転する間に4回、正六角形でやると6回、正方形でないひし形でやると2回、もとの図形にぴったり重なります。こういうのを「回転対称性」といいます。
この回転させる中心の点は、立体図形だと直線になります。その直線こそが対称軸です。立体をある線を中心に360°回す間に、もとの立体とn回重なれば、その立体はn回対称軸をもつということになります。
結晶では、2回対称軸●、3回対称軸▲、4回対称軸■、6回対称軸◆が多く見られます。
正八面体のもつ対称軸は,
対向する頂点をつなぐ4回対称軸が(頂点が6つあるので対向する頂点が3組あるため)3本。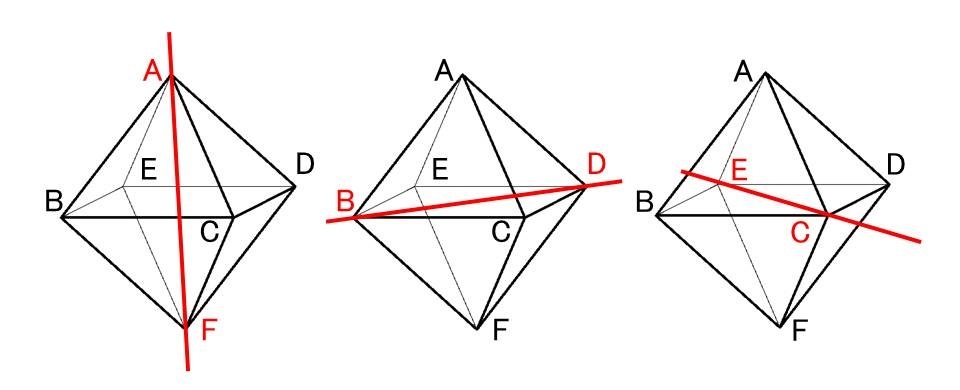
対向する面の中心をつなぐ3回対称軸が(面が8つあるので対向する面が4組あるため)4本,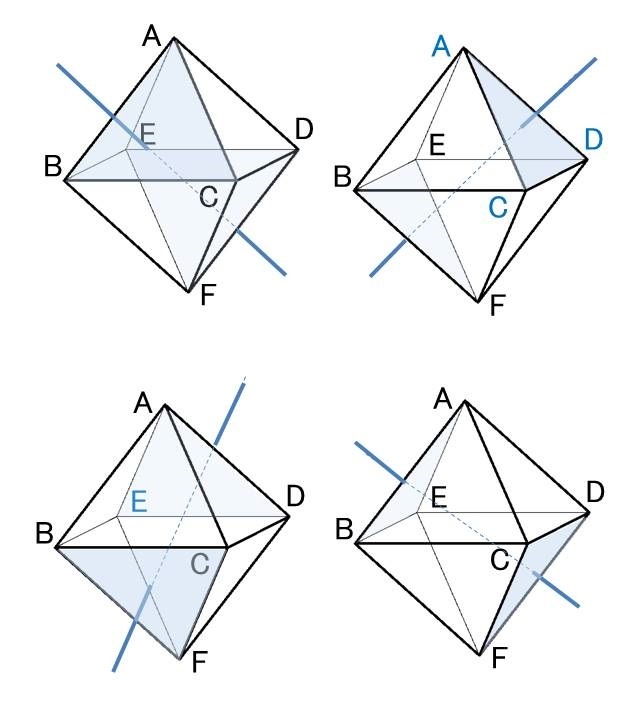
対向する辺の中心をつなぐ2回対称軸が(辺が12本あるので対向する辺が8組あるため)6本あります。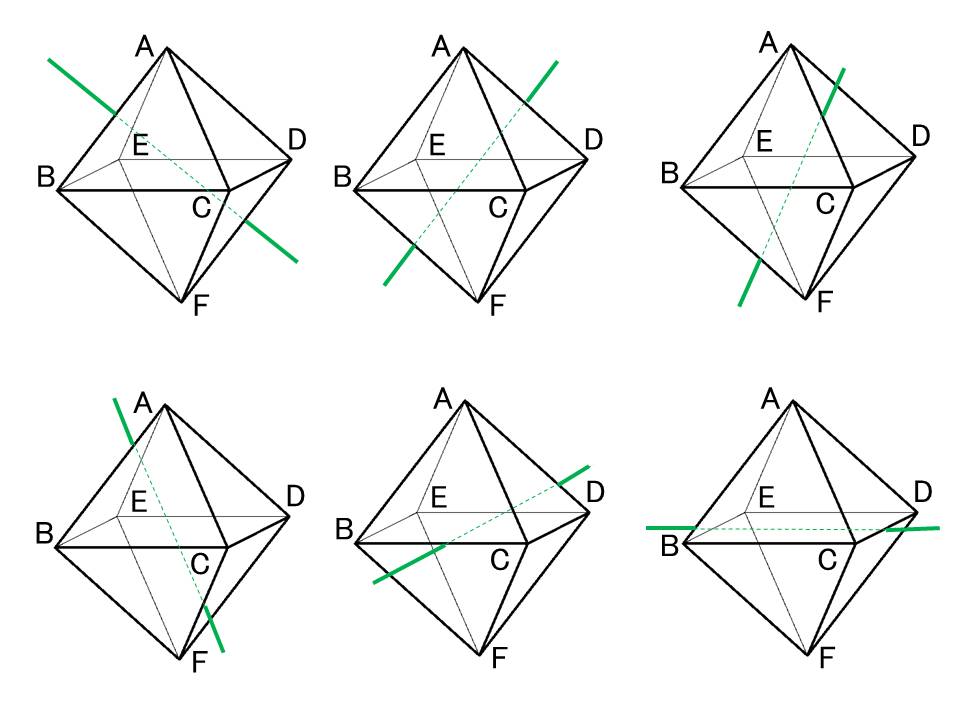
対称心
点対称な平面図形は、対応する2つの点を結ぶ直線が、対称の中心を通り、対称の中心から対応する2つの点までの長さは等しくなっています。
ところで下の図を見てくれ。こいつをどう思う?
すごく…懐かしい…です…。
懐かしいのはいいからさ、真ん中の赤い点が対称の中心です。
この性質を立体でやったとき、「対称の中心」が対称心です。
正八面体にも、対称心はあります。
対向する頂点を結ぶ3本の線が重なったところが、対称心になります。もちろん、1つしかありません。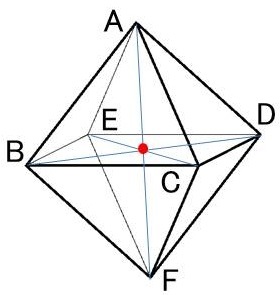
対称操作としては、他に回映があります。回映とは、一言でいうと、回転+鏡映で、もう少し詳しく言うと、ある軸のまわりに回転し,引き続いてその軸に垂直な面に関して鏡映の操作を続けて行うことです。なお、このときの回転軸が回映軸です。
ちなみに今回使った正八面体の対称面や対称軸などの図はパワポでつくったもので、下からダウンロードできますので、好きに使ってください。改変もOKです。

コメント