今年も共通テストの季節がやってまいりました。大学入試問題の中から中学校理科の知識・技能と思考力・判断力・表現力で解ける問題を取り上げていく企画です。
とくに共通テストになって、思考・判断・表現力に重点を置いたために、知識面については逆に中学校理科で学習した範囲で収まってしまうなんてことが起こっており、それを丁寧に拾ってみました。
2回目のこの記事では「物理基礎」から取り上げます。
そうそう、今年から「試験終了後であっても、大学入学共通テストの試験問題をSNSに投稿する等、インターネット上に掲載することはしないでください。という注意事項が加わりました。
なので、大学入試センターのサイトにある問題pdfへリンクを張ろうかと思ったのですが、まだアップされてないこともあるのですが、センターのサイトには過去3年までしか載っていないので、4年後にリンク切れになると問題が分からなくて困るな…と思ったので却下しました。
本ブログでは、
①共通テストでも中学校の理科で解ける問題があることを示すために引用の「必然性」がある
②引用する部分は色付きの背景にして明確に区別している
③あくまでも中学校の理科で解けるよという解説がメインで問題がサブという「主従関係」
④引用は当該問題のみと必要最小限度
⑤出典はさんざん大学入学共通テストの問題だよと示している
というかたちで、著作権法を意識しながら、大学入試センターの公表された著作物である試験問題を「引用」して利用しております。
物理基礎
第1問
問3 放射線と放射能について勉強をしている二人の高校生が会話している。次の会話文中の空欄[エ]~[カ]に入れる語の組合せとして最も適当なものを、後の①~⑥のうちから一つ選べ。
A:単位のベクレルとシーベルトはどう違うのでしょうか。
B:放射線を出す物質の放射能の強さを,1秒間に[エ]する[オ]の個数で表すのがベクレルですね。
A:では,シーベルトは放射線を受ける物質に関する単位ですか。
B:はい。シーベルトは. 物質が1 kgあたりに吸収するエネルギーに,放射線が[カ]へ及ぼす影響の違いを考慮した係数をかけた量の単位です。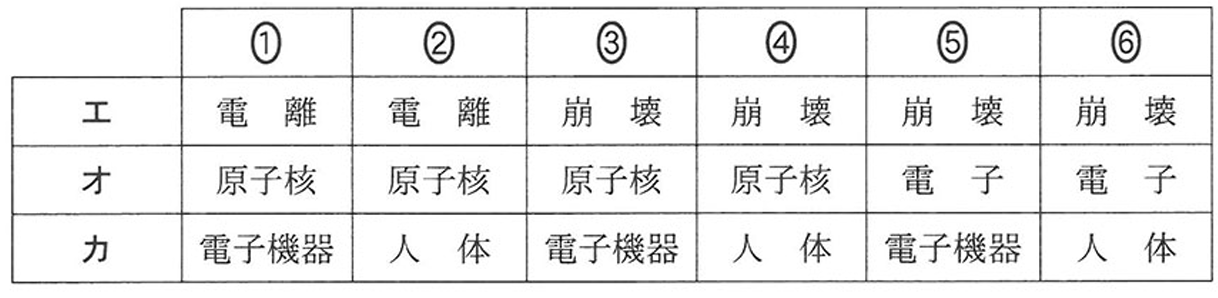
問3 放射線の単位、ベクレルとシーベルトについての知識に関する問題ですが、中学校3年生の教科書にも触れられています。
原子核が崩壊して放射線が発生すること、シーベルトは受けた放射線の人体に対する影響を表したものです。 ④
ちなみに、特に3・11から数年の間は、教科書よりもニュースなどでベクレルやシーベルトという単位が当たり前のように使われていましたが、村井 健志:放射線教育の現状と放射線に関する意識調査,INSS JOURNAL Vol. 20 SR-3,pp.28-37(2013)の調査では「放射線が人体に影響を表す単位としてベクレルが用いられる」という知識の正誤を満 20 歳以上の男女を対象に尋ねてみましたが、その回答は52%が「正しい」、15%が「正しくない」、33%が「わからない」「無回答」という結果でした。放射線が人体に影響を表す単位はベクレルではなくシーベルトですから、正しく理解できていた人は15%、そして半数以上の52%が自信をもって間違えていたということがわかります。
かと思えば、地震の授業でマグニチュードと震度の話をしたとき、「つまりマグニチュードはベクレル、震度はシーベルトみたいなものですね」という趣旨の反応をする中1がいて、いろんな意味でビビりました。
問4 次の文章中の空欄[キ]~[ケ]に入れる数値の組合せとして最も適当なものを,後の①~⑥のうちから一つ選べ。
運動会やダンスのマスゲーム(集団演技)などで見られる「ウェーブ」は,図2 のように,等間隔で横一列に並んだ人がタイミングを合わせて両手を上げて立ったり両手を下げて座ったりすることを繰り返し,全体として波のような動きを作り出す演技である。このウェーブを波動とみなし,その特徴を調べてみよう。
図2の破線は,ある瞬間とその0. 25s後における波長4.0 mのウェーブの一部を表したものである。各人が紙面の左側にいる人の動きのまねをすること によって,ウェーブが紙面の左から右に伝わるとする。人と人の問隔を 50 cm,ある人が隣の人の動きを0. 25 s後に再現するとすれば,ウェーブの速さは[キ]m/sとなる。また,ウェーブの振動数は[ク]Hzであり,ある人が手を下げて座った状態から. 手を上げて立ち上がり,再び手を下げて座った状態に戻るまでに[ク]sかかる。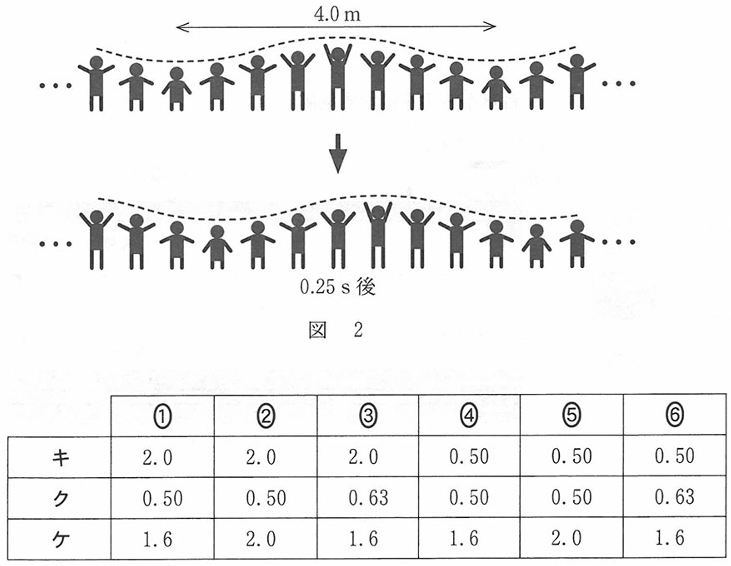
問4 何か難しい計算問題のような気がしますが、この話の本質は速さの問題です。キとケは完全に速さの公式の問題、クのHzは、音のところで学習した1秒間に何回振動したか、という話です。
ウェーブの速さは、図2の上の真ん中の人がいちばん手を上げて立ち上がっていますが、0.25秒後の図2の下の図では、いちばん手を上げて立ち上がっているのは、50cm離れた隣の人です。つまりいちばん手を上げて立ち上がっている状態(波でいえば山のところ)は0.25秒で50cm動いたわけです。これが波の速さになりますから、0.5m÷0.25s=2.0m/s
振動数、つまり、1秒間に波がいくつ通過するかということです。波の長さが4mで波の速さが2.0m/s、ということは1回の波が通過するのに4m÷2.0m/s=2.0sかかるということ。2秒で1回、つまり1秒間に0.5回ということになります。
ここでは、本来なら(高校なら)v=fλに代入して2.0m/s=f・4.0m からf=0.5と出していくかと思うのですが、中学生向けに4と2という数字ということもあって、1回に何秒かかるかという振動数の逆数を経由して出してみました。つまり、わかってやっています。
ある人が手を下げて座った状態から. 手を上げて立ち上がり,再び手を下げて座った状態に戻るまでの時間というのはさっき計算した1回の波が通過する時間、つまり2.0sとなります。 ②
第2問
台車の直線運動についての実験に関する次の文章を読み後の問い(問1~4)に答えよ。
Aさんは、磁石とスマートフォンの計測用アプリを使って、水平に置かれたレールの上をなめらかに動く台車(力学台車)の運動を調ぺようと考えた。実験に使う計測用アブリは、スマートフォンに内蔵されたセンサーを利用してセンサーの位置での磁場(磁界)の強さを瞬時に計測し、計測した磁場の強さの時問変化をグラフに表示する機能がある。センサーの位置が台車の中央と一致するようにスマートフオンを固定した。ただし、磁場が台車の運動に与える影響や、運動する台車とスマートフォンに生じる電磁誘導の影響は無視できるものとする。また、空気抵抗も無視できるものとする。
はじめにN極をレール側に向けて円形磁石(図1 (a))をレールの近くに一つ設置した。図1 (b)は実験装置を横から見た図、また図1 (c)は上から見た図を表している。レールに沿って右向きを正の向きとしたx軸をとる。台車をレールの左端に置いて計測用アプリを起動した後手で台車にカを加え原点Oで手をはなした。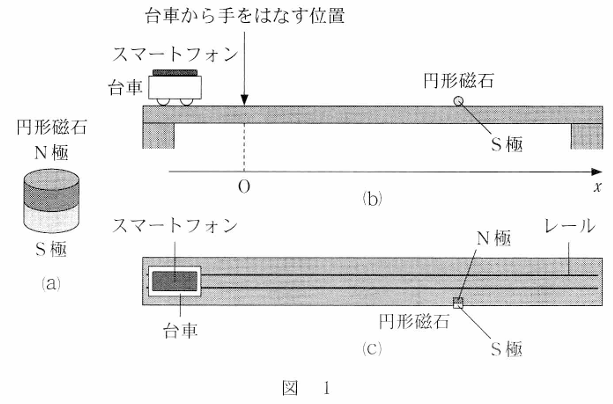
台車がレールの右端に到達したとき,図2 (a)のようなピークと幅を持つグラフが スマートフオンの画面に表示されていた。グラフの横軸は計測を開始した時刻を0 とした時刻,縦軸は磁場の強さを表している。また台車を動かす速さを変えて同じ実験を行ったところ,図2(b)のグラフが表示された。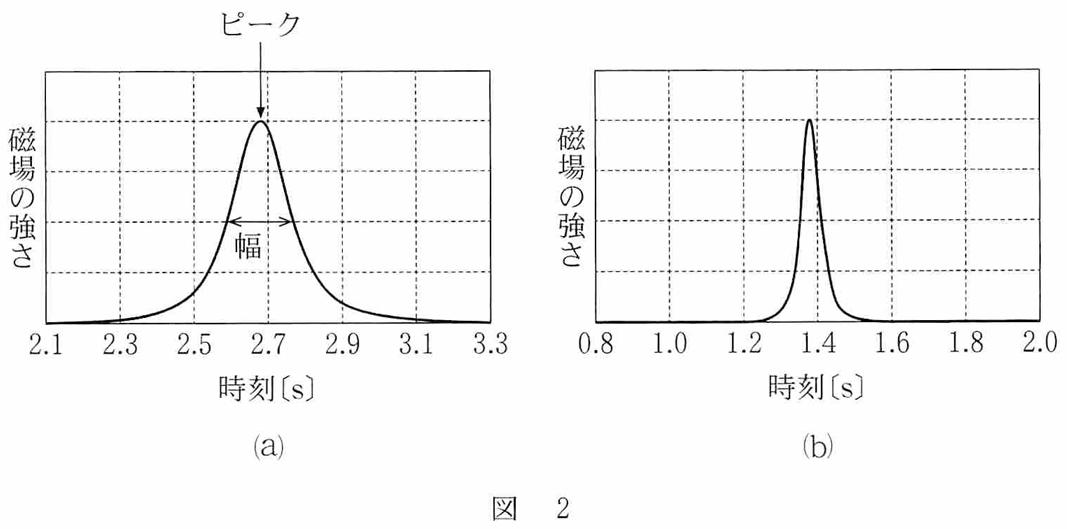
問1 次の文章中の空欄[ア]・[イ]に入れる数値と記号の組合せとして最も適当なものを、後の①~⑥のうちから一つ選べ。
図2(a)において、スマートフォンのセンサー部分が磁石のちょうど真横を通過した時刻は[ア]sである。また、台車の速さが大きいのは、図2の二つのグラフのうち[イ]の方である。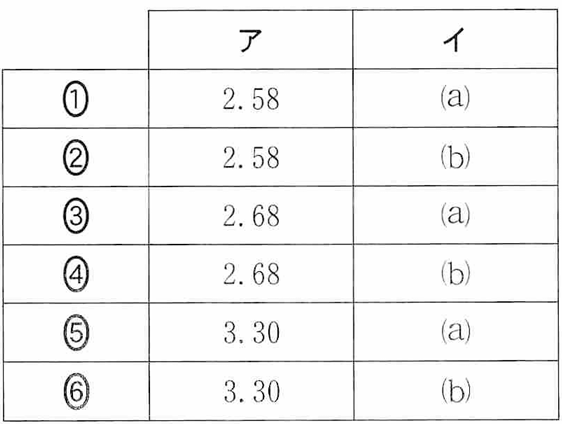
問1 磁石の真横にきたときが磁石とセンサーが最接近してグラフがピークになることが分かれば、あとはグラフの読み取り。横軸が0.2刻みなのに注意して、2.7のちょっと手前の2.68と読める。(2.58なら、2.5と2.7の真ん中よりも左寄りのはずである。)また動きが速いと磁石に速く近づき速く遠ざかるので、磁場の強さが急激に上がって急激に下がる。 ④
次に、図3のように、レールの近くに5個の同じ円形磁石を等間隔で設置した、円形磁石のN極はすべてレール側を向いている。円形磁石の位置をそれぞれx1,x2,x3,x4,x5とする。だおしゃをレールの左端において計測用アプリを起動した後、手で台車に力を加え、原点Oで手をはなした。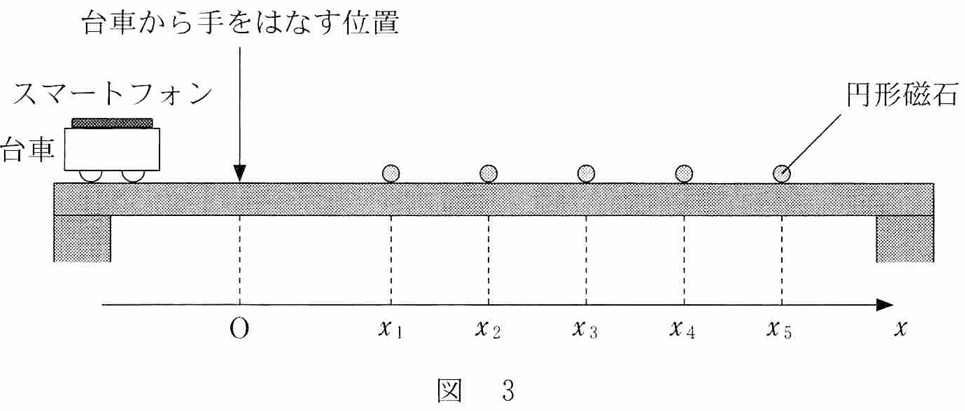
問2 この実験で台車がレールの右端に到達したとき、スマートフォンに表示されるグラフとして最も適当なものを、次の①~④のうちから一つ選べ。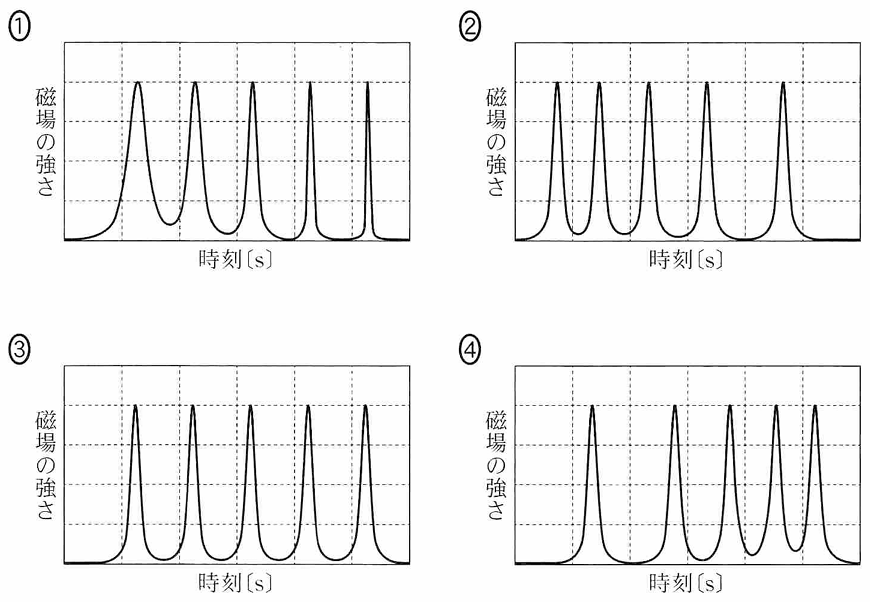
問2 台車にかかる力が釣り合っている状態で動いているので等速直線運動。したがってグラフは等間隔に同じ形のピークができる。 ③
今度は、5個の円形磁石は設置したまま、図4のように、伸び縮みしない軽い糸の一端を台車に取りつけ、他端をなめらかに回る軽い滑車を通しておもりにつないだ。原点Oの位置に台車を制止させ、計測用アプリを起動した後、静かに手をはなした。ただし、台車がレールの右端に到達するまでおもりは落下し続けるものとする。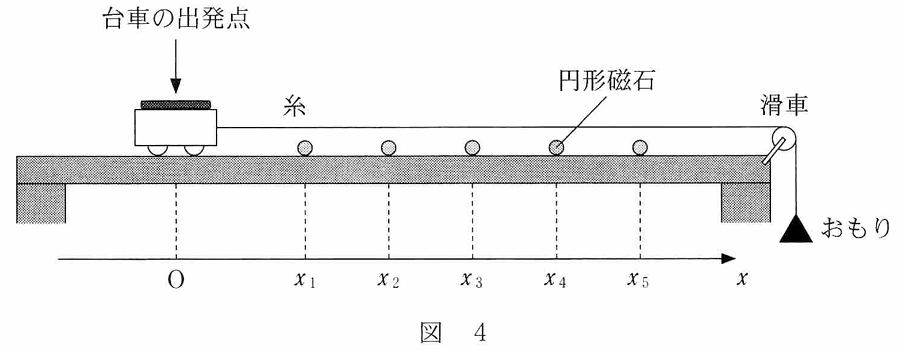
問3 この実験で台車がレールの右端に到達したとき、スマートフォンに表示されるグラフとして最も適当なものを、次の①~④のうちから一つ選べ。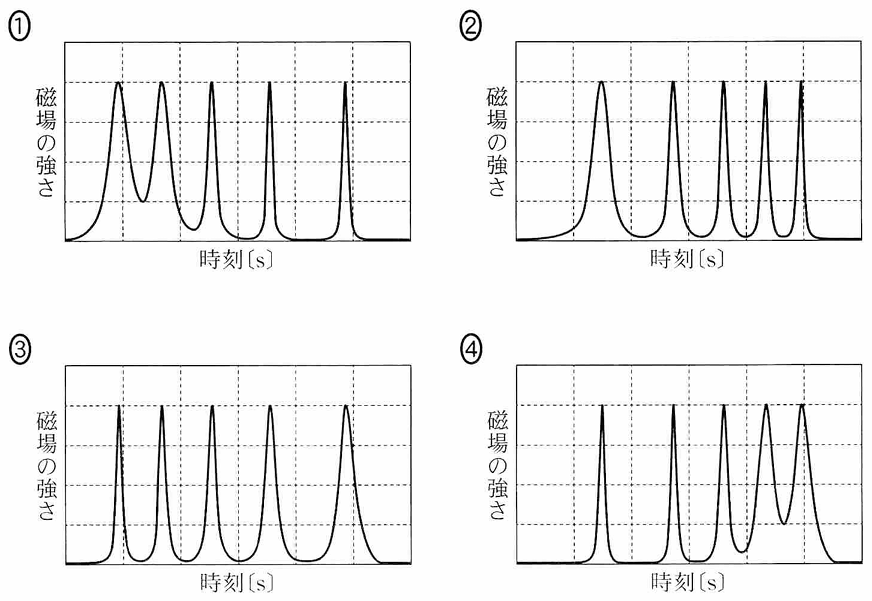
問3 今度はおもりによって台車の進行方向に一定の大きさの力が加わっているため、だんだん速くなっていく。つまりこれは斜面を下る運動と同じパターンになる。なのでグラフではピークの間隔がだんだん狭くなっていく。 ②
第3問
問3 図1 のOP問の電圧を表す式として最も適当なものを,後の①-⑥のうちからーつ選べ。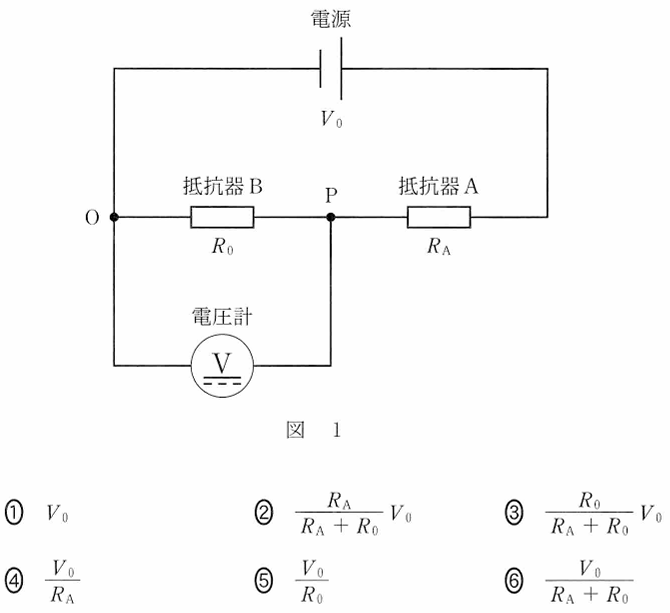
問3 直列回路なので、電流は回路のどこでも一定で、I=Vo/(R0+Ra)となる。この電流に抵抗器Bの抵抗R0をかけた R0・Vo/(R0+Ra)が抵抗器Bの両端にかかる電圧。 ③
ちなみに問3の前に、数行のリード文があったのですが、スルーしても解答には全く影響がなかった…。
図2のように比熱を測定する試料をのせる試料台に図1に示した抵抗器A を取りつけ,電圧Vの電源をつないだヒーターで試料台と試料を加熱する。 ヒーターの抵抗値は温度によらず常にRでありヒーターで発生したジュール 熱はすべて試料台と試料の温度上昇に使われるものとする。また抵抗器A の 熱容量とそこで発生するジュール熱は無視できるものとし,試料台,試料,および抵抗器Aの温度は互いに等しいものとする。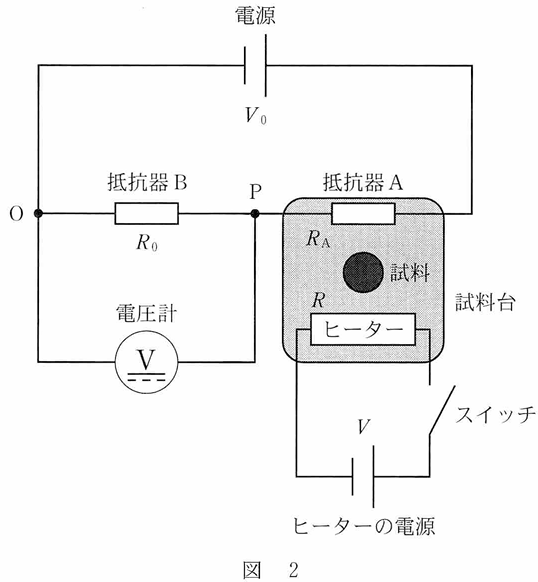
試料をのせないで試料台を加熱する予備測定と,試料をのせた試料台を加熱する本測定を行う。二つの測定は,温度が同じ状態から開始する。試料をのせない予備測定では,時問tだけ加熱したところ,試料台の温度はΔTだけ上昇した。 試料をのせた本測定では,試料台の熱容量に試料の熱容量が加わったため,試料と試料台の温度が同じΔTだけ上昇するのに必要な加熱時間は増加し,t'(t’> t) となった。
問4 予備測定において、ヒーターで発生した熱量Qを表す式として最も適当なものを、次の①~⑥のうちから一つ選べ。Q=[113]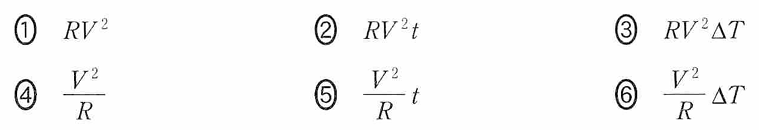
問4 発熱量Q=電力P×時間t 電力P=電圧V×電流I I=V/Rだから P=V2/R
Q=V2/R・t ⑤
問4を解くだけだったら、単に電圧V、抵抗Rで時問tだけ加熱したところ,試料台の温度はΔTだけ上昇した。さて発熱量Qは?という話で済んだのですが、この後の問5に直結するので、つらつらと問4には不要な情報が…。
物理基礎のまとめ
物理基礎14問50点中、中学校理科で解ける問題は、なんと7問26点分と点数でいえば半分以上を占めていました。残りの問題も、たとえば比熱がらみの問題なんかは、現在の中学校の教科書(現行の学習指導要領)には載っていないというだけで、有名中学を受験する小学校のお子さんなら数式の処理はできなくても具体的な数値があったら解答できそうなものもあります。
たしかに数式を文字式のまま計算したりするのは苦手な人が多いかもしれませんが、本質は意外にわかってしまえば簡単なことかもしれません。でもそういう人は理系に行くから、共通テストで物理基礎なんて選択しないで、ガチの物理を解答するのでしょうが…。

コメント